Зміст

Одним з показників, що описують якість побудованої моделі в статистиці, є коефіцієнт детермінації (R^2), який ще називають величиною достовірності апроксимації. З його допомогою можна визначити рівень точності прогнозу. Давайте дізнаємося, як можна зробити розрахунок даного показника за допомогою різних інструментів програми Excel.
Обчислення коефіцієнта детермінації
В залежності від рівня коефіцієнта детермінації, прийнято розділяти моделі на три групи:
| 0,8 – 1 | Модель хорошої якості |
| 0,5 – 0,8 | модель прийнятної якості |
| 0 – 0,5 | модель поганої якості |
В останньому випадку якість моделі говорить про неможливість її використання для прогнозу.
Вибір способу обчислення зазначеного значення в Excel залежить від того, чи є регресія лінійною чи ні. У першому випадку можна використовувати функцію КВПІРСОН , а в другому доведеться скористатися спеціальним інструментом з пакету аналізу.
Спосіб 1: обчислення коефіцієнта детермінації при лінійній функції
Перш за все, з'ясуємо, як знайти коефіцієнт детермінації при лінійній функції. В цьому випадку даний показник буде дорівнювати квадрату коефіцієнта кореляції. Зробимо його розрахунок за допомогою вбудованої функції Excel на прикладі конкретної таблиці, яка наведена нижче.
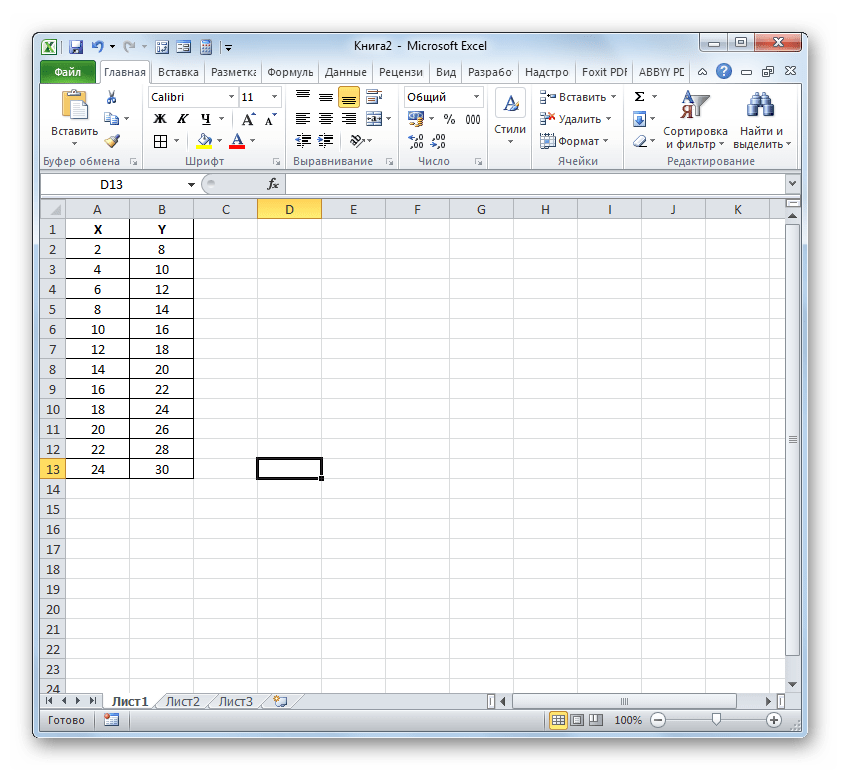
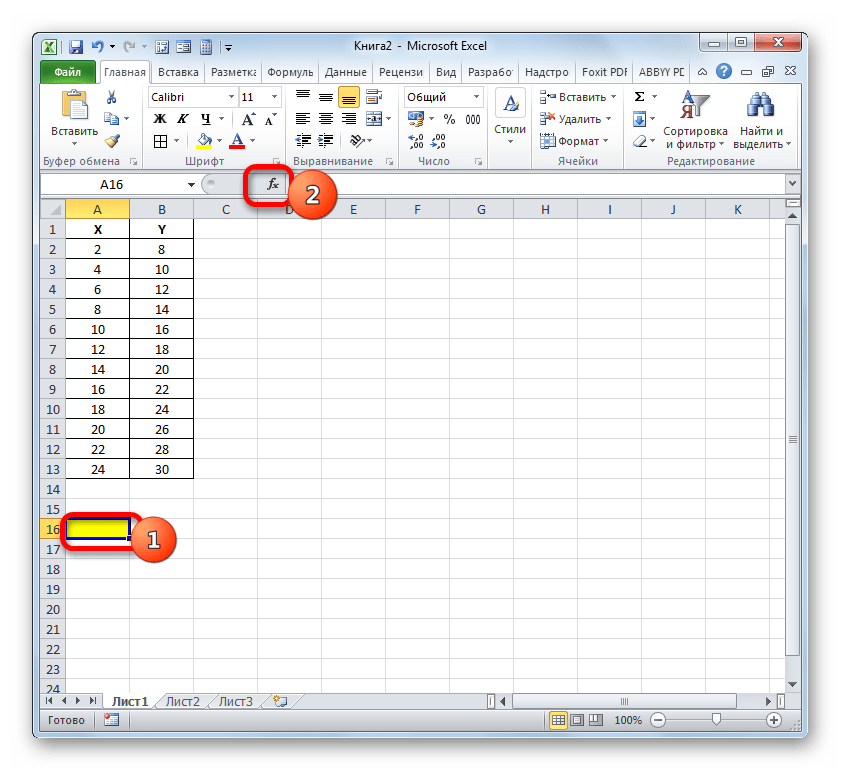
- Виділяємо осередок, де буде проведений висновок коефіцієнта детермінації після його розрахунку, і клацаємо по піктограмі " Вставити функцію» .
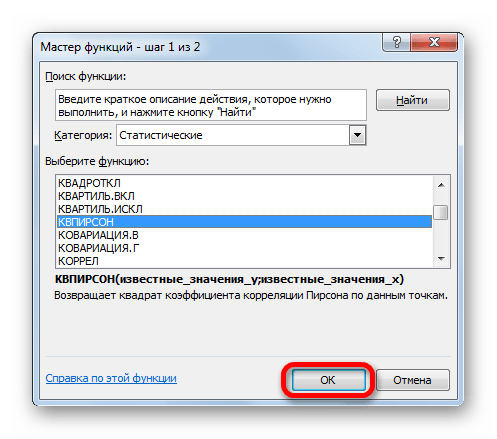
- Запускається Майстер функцій . Переміщаємося в його категорію »статистичні" і відзначаємо найменування " КВПІРСОН» . Далі клацаємо по кнопці «OK» .
- Відбувається запуск вікна аргументів функції КВПІРСОН
. Даний оператор зі статистичної групи призначений для обчислення квадрата коефіцієнта кореляції функції Пірсона, тобто, лінійної функції. А як ми пам'ятаємо, при лінійної функції коефіцієнт детермінації якраз дорівнює квадрату коефіцієнта кореляції.
Синтаксис цього оператора такий:
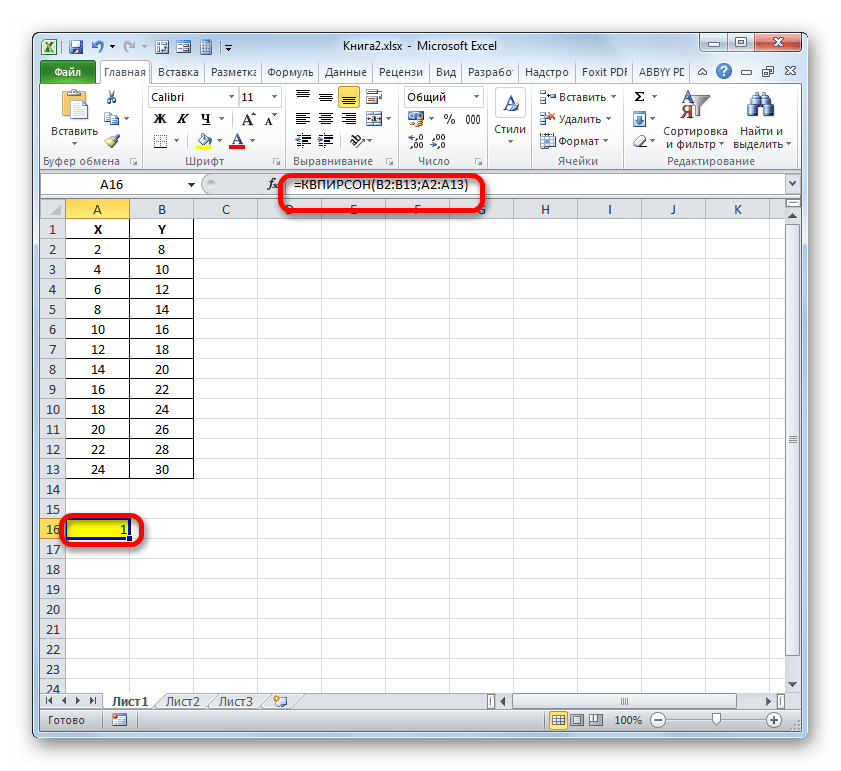
=КВПІРСОН(відомі_значення_у; відомі_значення_х)Таким чином, функція має два оператори, один з яких є переліком значень функції, а другий – аргументів. Оператори можуть бути представлені, як безпосередньо у вигляді значень, перерахованих через крапку з комою ( ; ), так і у вигляді посилань на діапазони, де вони розташовані. Саме останній варіант і буде використаний нами в даному прикладі.
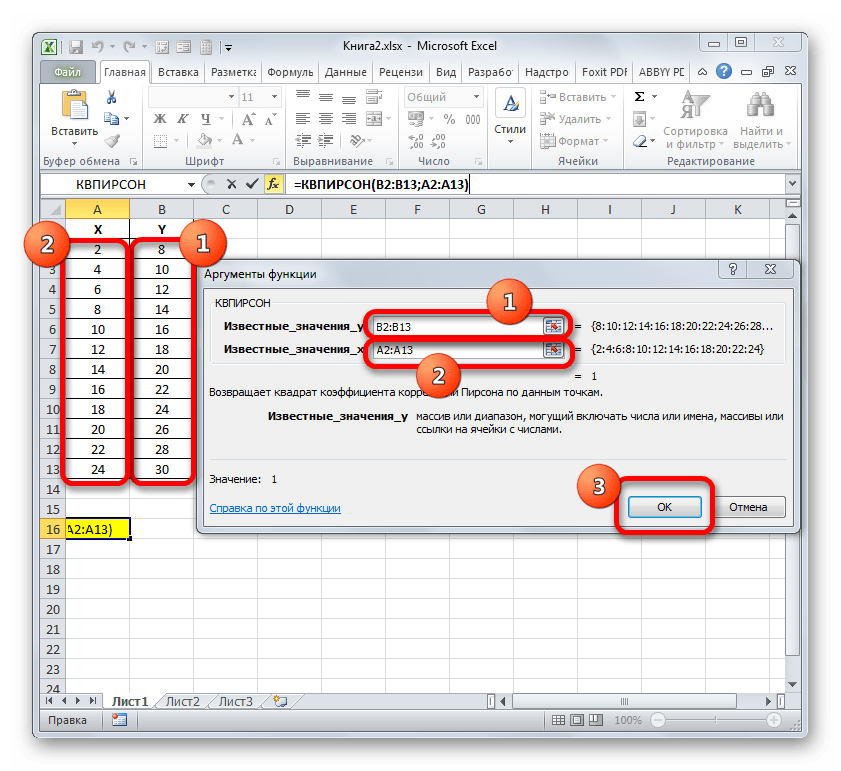
Встановлюємо курсор в поле " відомі значення y» . Виконуємо затиск лівої кнопки мишки і виробляємо виділення вмісту стовпця «Y» таблиці. Як бачимо, адреса зазначеного масиву даних тут же відображається у вікні.
Аналогічним чином заповнюємо поле " відомі значення x» . Ставимо курсор в дане поле, але на цей раз виділяємо значення стовпця «X» .
Після того, як всі дані були відображені у вікні аргументів КВПІРСОН , клацаємо по кнопці «OK» , розташованої в самому його низу.
- Як бачимо, слідом за цим програма виробляє розрахунок коефіцієнта детермінації і видає результат в ту клітинку, яка була виділена ще перед викликом майстри функцій . У нашому прикладі значення обчислюваного показника вийшло рівним 1. Це означає, що представлена модель абсолютно достовірна, тобто, виключає похибку.
Урок: Майстер функцій у Microsoft Excel
Спосіб 2: обчислення коефіцієнта детермінації в нелінійних функціях
Але зазначений вище варіант розрахунку шуканого значення можна застосовувати тільки до лінійних функцій. Що ж робити, щоб зробити його розрахунок в нелінійної функції? В Ексель є і така можливість. Її можна здійснити за допомогою інструменту «регресія» , який є складовою частиною пакета " аналіз даних» .
- Але перш, ніж скористатися зазначеним інструментом, слід активувати сам " Пакет аналізу» , який за замовчуванням в Ексель відключений. Переміщаємося у вкладку »Файл" , а потім переходимо по пункту »Параметри" .
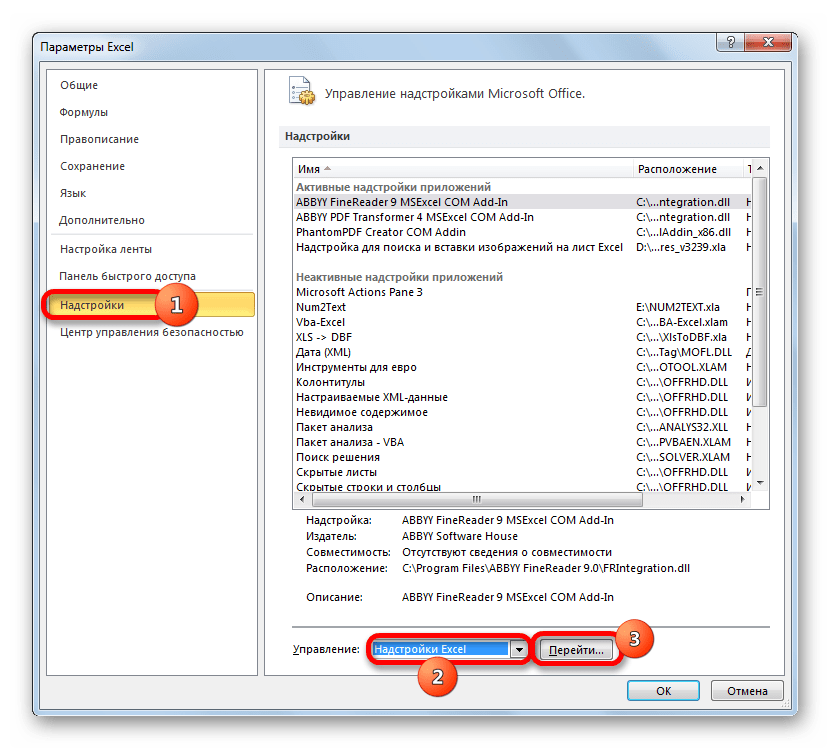
- У вікні виробляємо переміщення в розділ «надбудови» за допомогою навігації по лівому вертикальному меню. У нижній частині правої області вікна розташовується поле «Управління» . Зі списку доступних там підрозділів вибираємо найменування " Надбудови Excel ... » , а потім клацаємо по кнопці " Перейти...» , розташованої праворуч від поля.
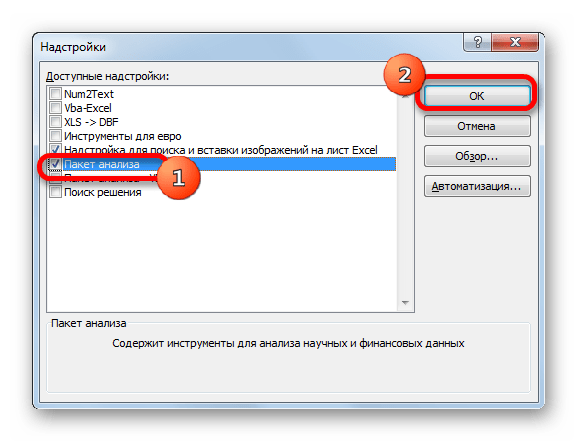
- Проводиться запуск вікна надбудов. У центральній його частині розташований список доступних надбудов. Встановлюємо прапорець біля позиції " Пакет аналізу» . Слідом за цим потрібно клацнути по кнопці «OK» у правій частині інтерфейсу вікна.
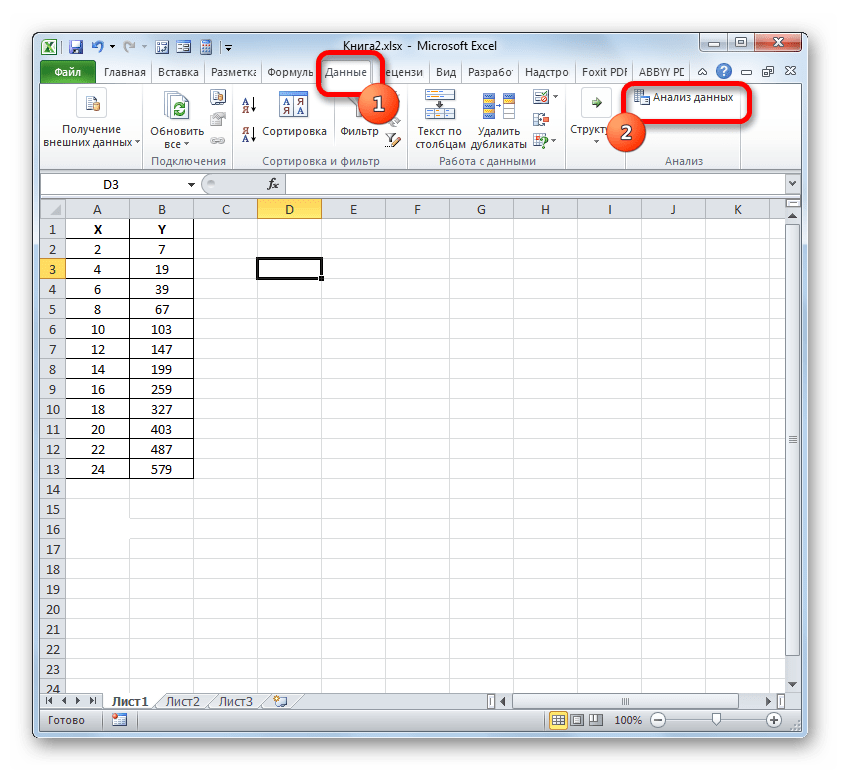
- Пакет інструментів " аналіз даних» у поточному екземплярі Excel буде активовано. Доступ до нього розташовується на стрічці у вкладці »дані" . Переміщаємося в зазначену вкладку і клацаємо по кнопці " аналіз даних» у групі налаштувань " аналіз» .
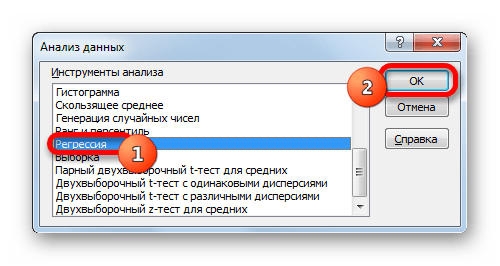
- Активується віконце " аналіз даних» зі списком профільних інструментів обробки інформації. Виділяємо з цього переліку пункт «регресія» і клацаємо по кнопці «OK» .
- Потім відкривається вікно інструменту «регресія»
. Перший блок налаштувань –
" вхідні дані»
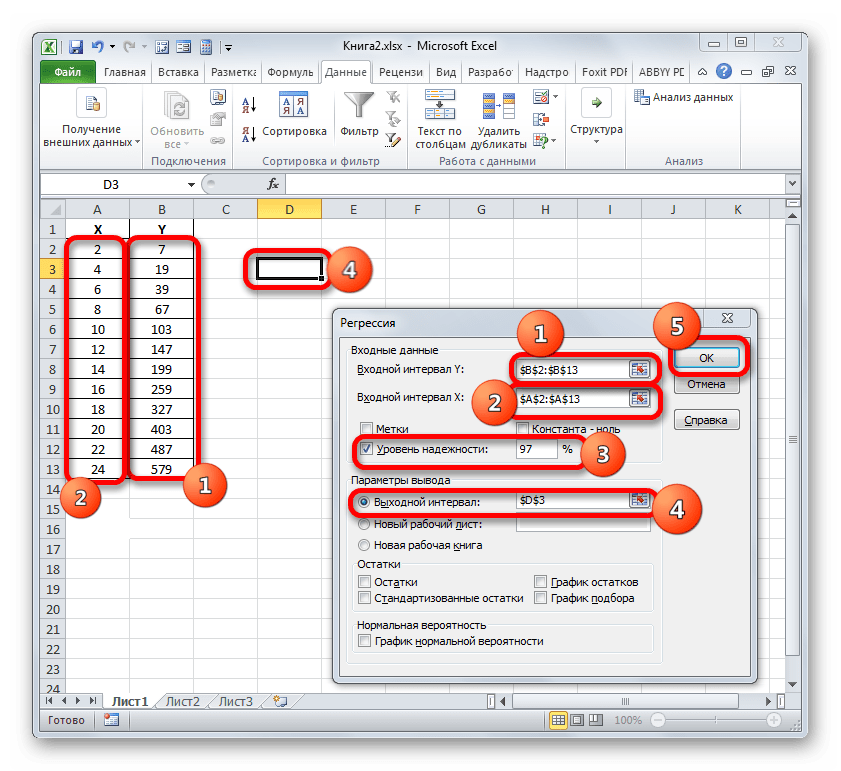
. Тут в двох полях потрібно вказати адреси діапазонів, де знаходяться значення аргументу і функції. Ставимо курсор в поле
«вхідний інтервал Y»
і виділяємо на аркуші вміст колонки
«Y»
. Після того, як адреса масиву відображається у вікні
«регресія»
, ставимо курсор в поле
«вхідний інтервал Y»
і точно таким же чином виділяємо осередки стовпця
«X»
.
Про параметри " мітка» і «Константа-нуль» прапорці не ставимо. Прапорець можна встановити близько параметра " рівень надійності» і в поле навпроти вказати бажану величину відповідного показника (за замовчуванням 95%).
У групі «параметри виводу» потрібно вказати, в якій області буде відображатися результат обчислення. Існує три варіанти:
- Область на поточному аркуші;
- Інший лист;
- Інша книга (новий файл).
Зупинимо свій вибір на першому варіанті, щоб Вихідні дані і результат розміщувалися на одному робочому аркуші. Ставимо перемикач близько параметра " вихідний інтервал» . В поле навпроти даного пункту ставимо курсор. Клацаємо лівою кнопкою миші по порожньому елементу на аркуші, який покликаний стати лівою верхньою коміркою таблиці виведення підсумків розрахунку. Адреса даного елемента повинен висвітитися в поле вікна «регресія» .
Групи параметрів»залишки" і " нормальна ймовірність» ігноруємо, так як для вирішення поставленого завдання вони не важливі. Після цього клацаємо по кнопці «OK» , яка розміщена в правому верхньому куті вікна «регресія» .
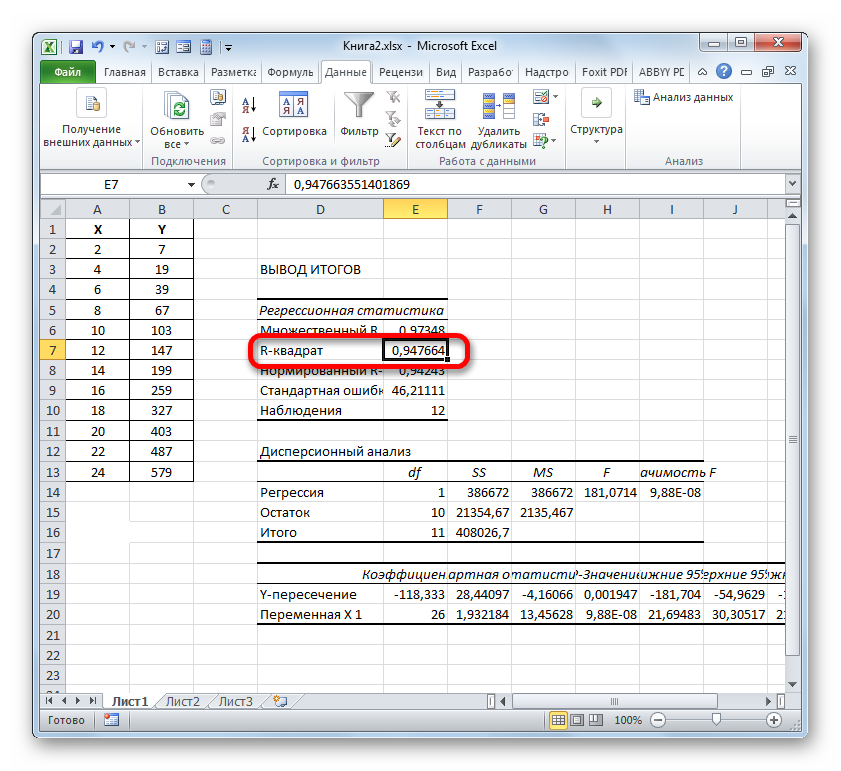
- Програма робить розрахунок на основі раніше введених даних і виводить результат в зазначений діапазон. Як бачимо, даний інструмент виводить на лист досить велика кількість результатів за різними параметрами. Але в контексті поточного уроку нас цікавить показник «R-квадрат» . В даному випадку він дорівнює 0,947664, що характеризує обрану модель, як модель хорошої якості.
Спосіб 3: коефіцієнт детермінації для лінії тренду
Крім зазначених вище варіантів, коефіцієнт детермінації можна відобразити безпосередньо для лінії тренда в графіку, побудованому на аркуші Excel. З'ясуємо, як це можна зробити на конкретному прикладі.
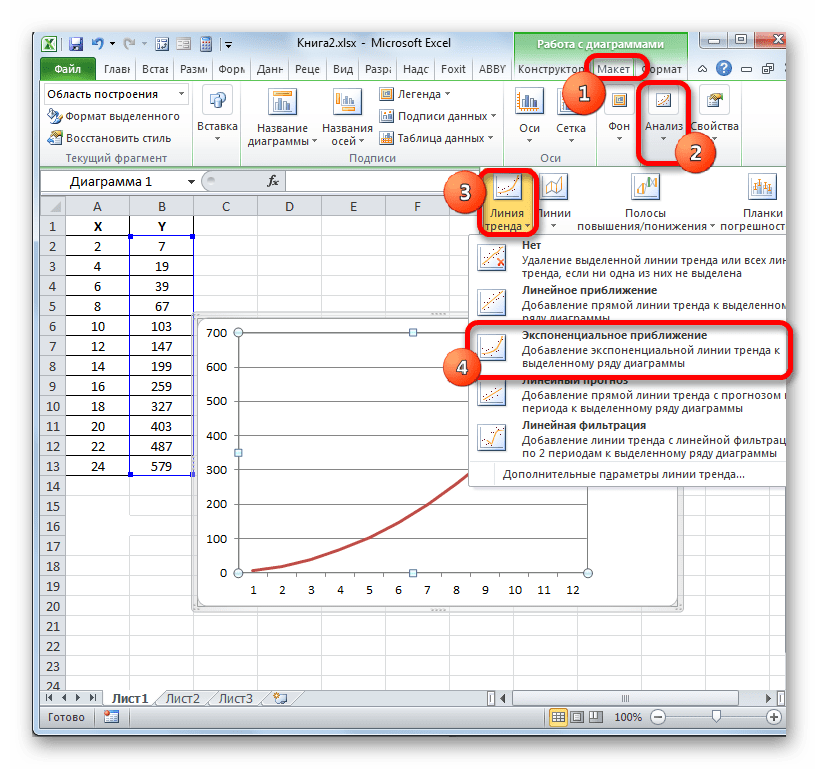
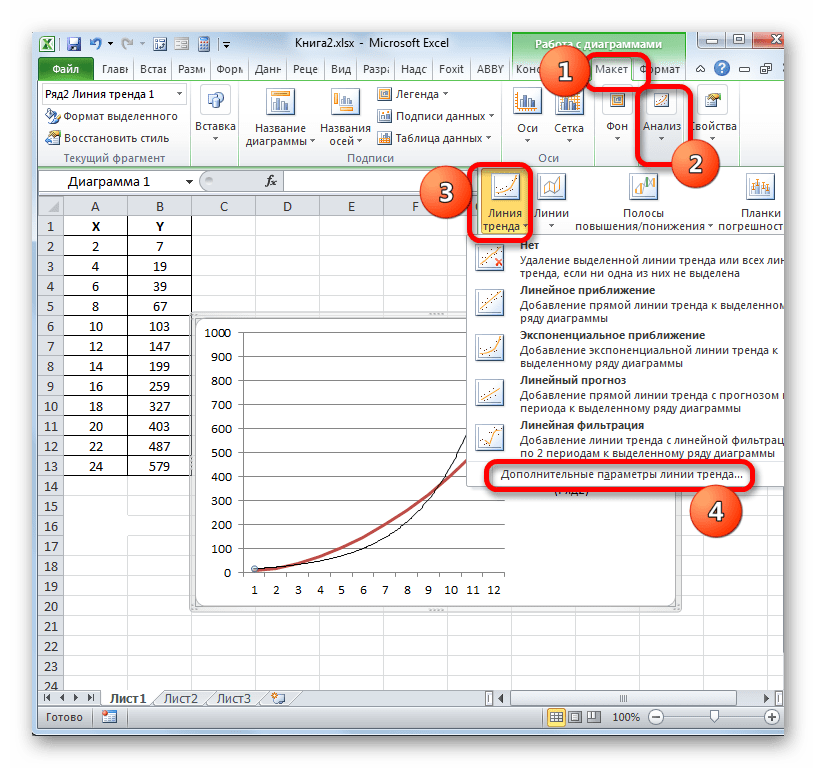
- Ми маємо графік, побудований на основі таблиці аргументів і значень функції, яка була використана для попереднього прикладу. Зробимо побудова до нього лінії тренда. Кількома по будь-якому місцю області побудови, на якій розміщений графік, лівою кнопкою миші. При цьому на стрічці з'являється додатковий набір вкладок – " робота з діаграмами» . Переходимо у вкладку »Макет" . Клацаємо по кнопці " лінія тренду» , яка розміщена в блоці інструментів " аналіз» . З'являється меню з вибором типу лінії тренда. Зупиняємо вибір на тому типі, який відповідає конкретній задачі. Давайте для нашого прикладу виберемо варіант " експоненціальне наближення» .
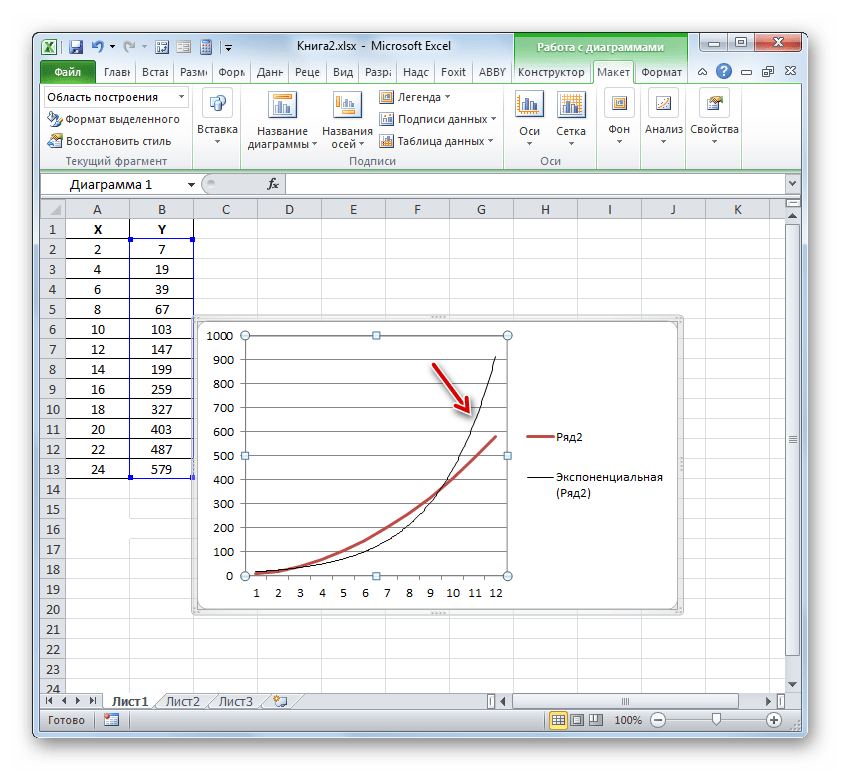
- Ексель будує прямо на площині побудови графіка лінію тренда у вигляді додаткової чорної кривої.
- Тепер нашим завданням є відобразити власне коефіцієнт детермінації. Кількома правою кнопкою миші по лінії тренда. Активується контекстне меню. Зупиняємо вибір в ньому на пункті " Формат лінії тренду...»
.
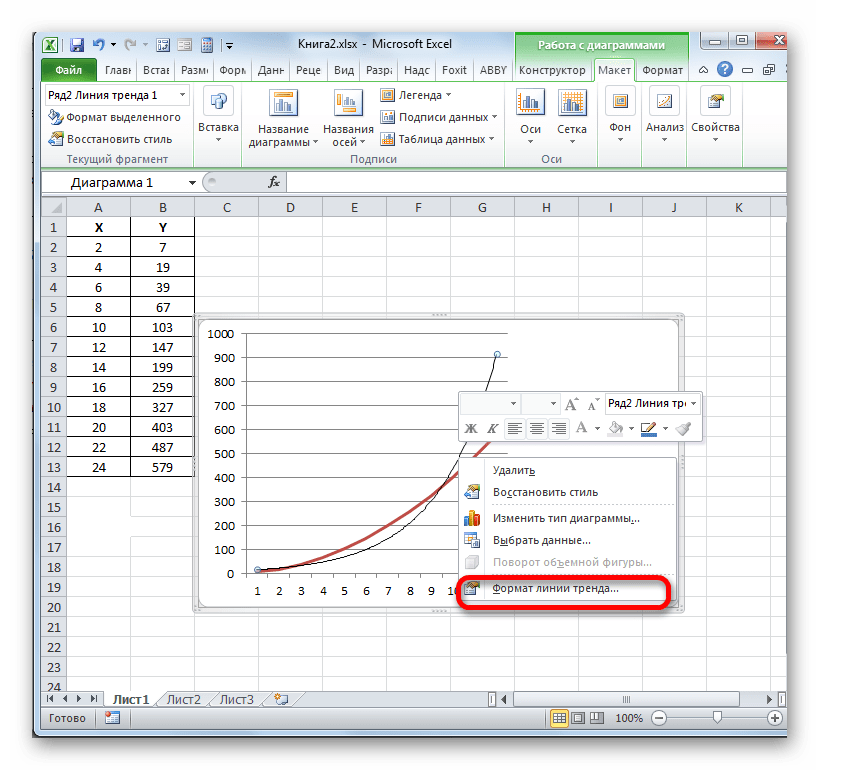
Для виконання переходу в вікно формату лінії тренда можна виконати альтернативну дію. Виділяємо лінію тренда кліком по ній лівої кнопки миші. Переміщаємося у вкладку «Макет» . Клацаємо по кнопці " лінія тренду» в блоці " аналіз» . У списку клацаємо по самому останньому пункту переліку дій – " Додаткові параметри лінії тренду...» .
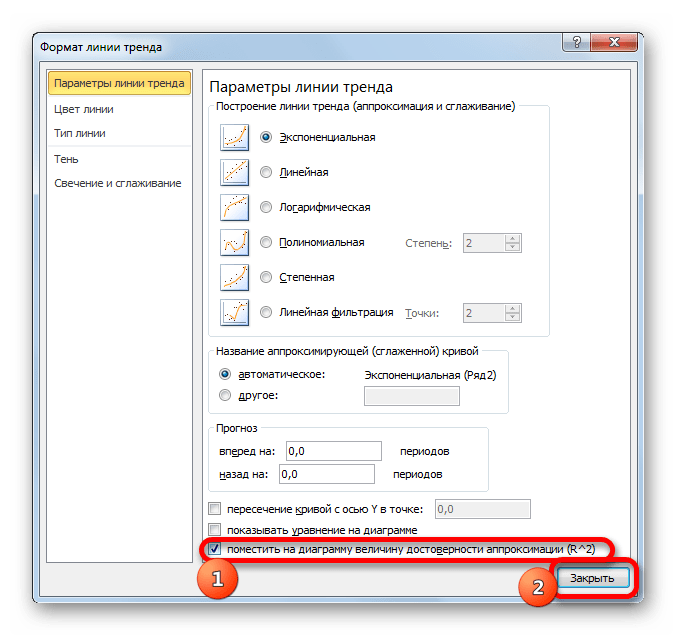
- Після будь-якого з двох вищевказаних дій запускається віконце формату, в якому можна зробити додаткові настройки. Зокрема, для виконання нашого завдання необхідно встановити прапорець навпроти пункту " помістити на діаграму величину достовірності апроксимації (R^2)» . Він розміщений в самому низу вікна. Тобто, таким чином ми включаємо відображення коефіцієнта детермінації на області побудови. Потім не забуваємо натиснути на кнопку »закрити" внизу поточного вікна.
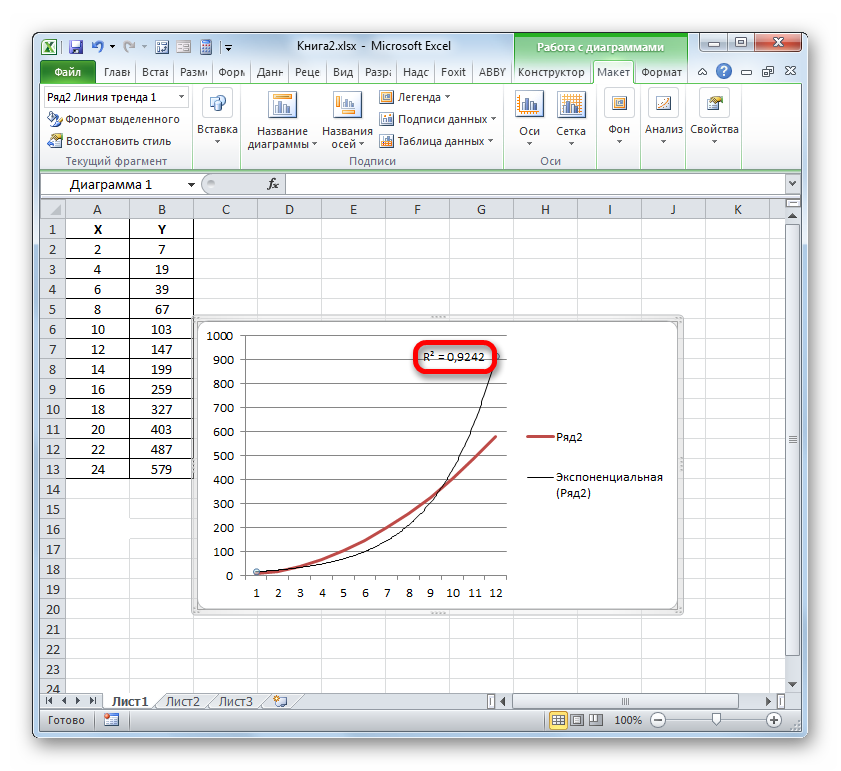
- Значення достовірності апроксимації, тобто, величина коефіцієнта детермінації, буде відображено на аркуші в області побудови. В даному випадку ця величина, як бачимо, дорівнює 0,9242, що характеризує апроксимацію, як модель хорошої якості.
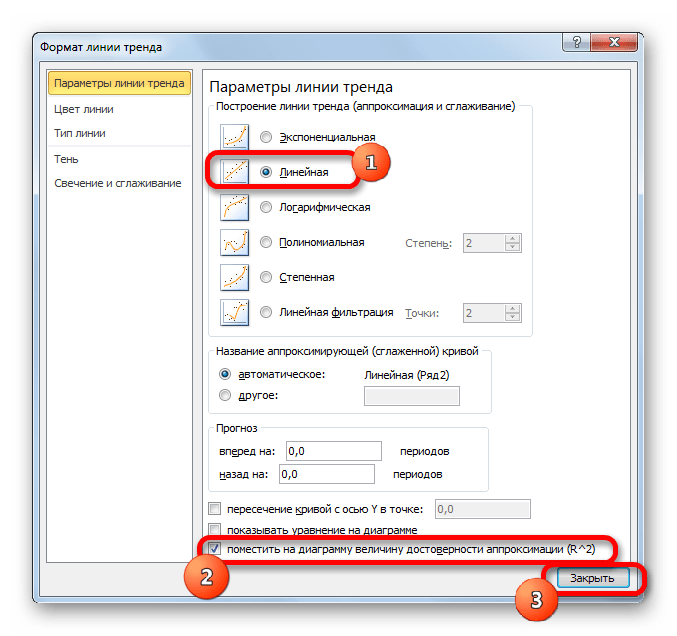
- Абсолютно точно таким чином можна встановлювати показ коефіцієнта детермінації для будь-якого іншого типу лінії тренда. Можна змінювати тип лінії тренда, зробивши перехід через кнопку на стрічці або контекстне меню у вікно її параметрів, як було показано вище. Потім вже в самому вікні в групі " побудова лінії тренду» можна переключитися на інший тип. Не забуваємо при цьому контролювати, щоб біля пункту " помістити на діаграму величину достовірності апроксимації» було встановлено прапорець. Завершивши вищевказані дії, клацаємо по кнопці »закрити" у нижньому правому куті вікна.
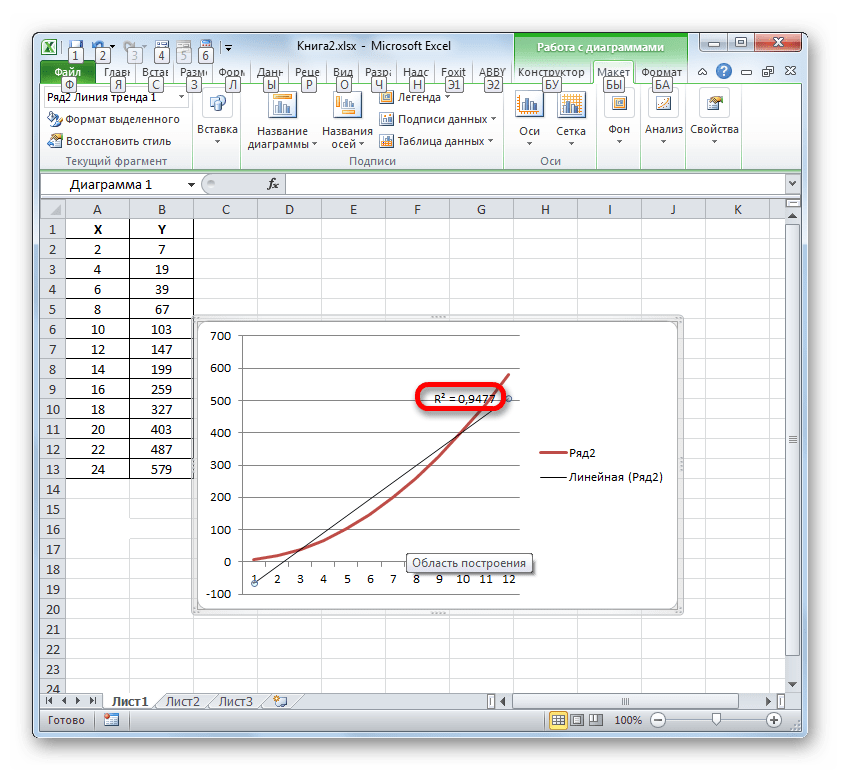
- При лінійному типі лінія тренда вже має значення достовірності апроксимації Рівне 0,9477, що характеризує цю модель, як ще більш достовірну, ніж розглянуту нами раніше лінію тренда експоненціального типу.
- Таким чином, перемикаючись між різними типами лінії тренда і порівнюючи їх значення достовірності апроксимації (коефіцієнт детермінації), можна знайти той варіант, модель якого найбільш точно описує представлений графік. Варіант з найвищим показником коефіцієнта детермінації буде найбільш достовірним. На його основі можна будувати найточніший прогноз.
Наприклад, для нашого випадку дослідним шляхом вдалося встановити, що найвищий рівень Достовірності має поліноміальний тип лінії тренда другого ступеня. Коефіцієнт детермінації в даному випадку дорівнює 1. Це говорить про те, що зазначена модель абсолютно достовірна, що означає повне виключення похибок.
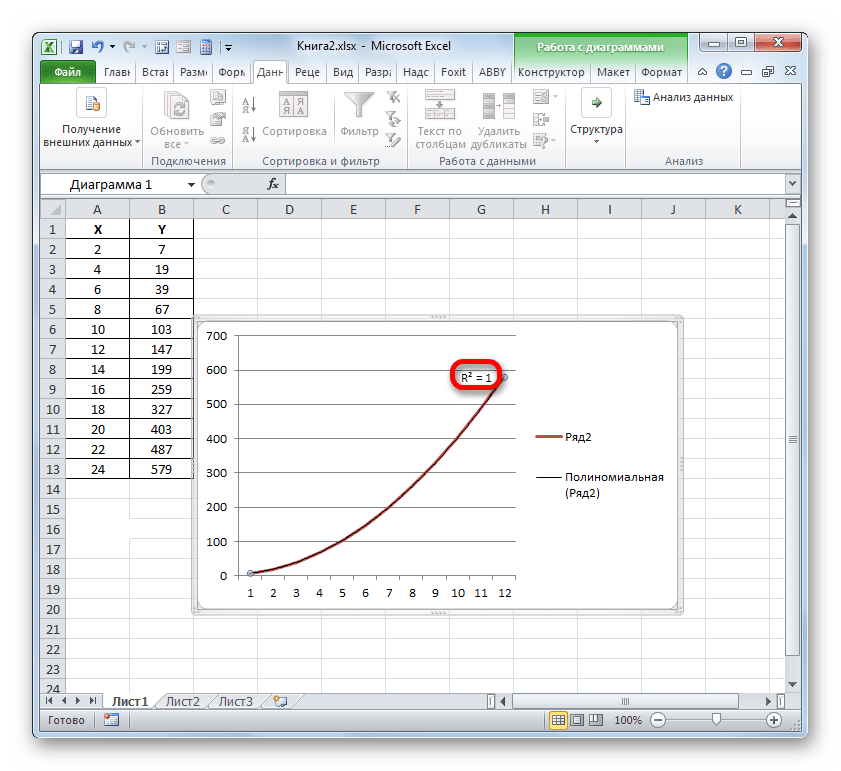
Але, в той же час, це зовсім не означає, що для іншого графіка теж найбільш достовірним виявиться саме цей тип лінії тренда. Оптимальний вибір типу лінії тренда залежить від типу функції, на підставі якої був побудований графік. Якщо Користувач не володіє достатнім обсягом знань, щоб «на око» прикинути найбільш якісний варіант, то єдиним виходом визначення кращого прогнозу є якраз порівняння коефіцієнтів детермінації, як було показано на прикладі вище.
Читайте також:
побудова лінії тренду в Excel
апроксимація в Excel
В Екселі існують два основних варіанти обчислення коефіцієнта детермінації: використання оператора КВПІРСОН і застосування інструменту «регресія» з набору інструментів «аналіз даних» . При цьому перший з цих варіантів призначений для використання тільки в процесі обробки лінійної функції, а інший варіант можна використовувати практично у всіх ситуаціях. Крім того, існує можливість відображення коефіцієнта детермінації для лінії трендів графіків в якості величини достовірності апроксимації. За допомогою даного показника є можливість визначити тип лінії тренда, який має найвищий рівень Достовірності для конкретної функції.




