застосування кластерного аналізу в Microsoft Excel

Зміст

• Використання кластерного аналізу
  • Приклад використання
• Питання та відповіді

Одним з інструментів для вирішення економічних завдань є кластерний аналіз. З його допомогою кластери та інші об'єкти масиву даних класифікуються за групами. Дану методику можна застосовувати в програмі Excel. Подивимося, як це робиться на практиці.

Використання кластерного аналізу

За допомогою кластерного аналізу можна проводити вибірку за ознакою, яка досліджується. Його основне завдання-розбиття багатовимірного масиву на однорідні групи. Як критерій угруповання застосовується парний коефіцієнт кореляції або евклідова відстань між об'єктами по заданому параметру. Найбільш близькі один до одного значення групуються разом.

Хоча найчастіше даний вид аналізу застосовують в економіці, його також можна використовувати в біології (для класифікації тварин), психології, медицині і в багатьох інших сферах діяльності людини. Кластерний аналіз можна застосовувати, використовуючи для цих цілей стандартний набір інструментів Ексель.

Приклад використання

Маємо п'ять об'єктів, які характеризуються за двома досліджуваними параметрами – x і y .

1. Застосовуємо до даних значень формулу евклідового відстані, яке обчислюється за шаблоном:

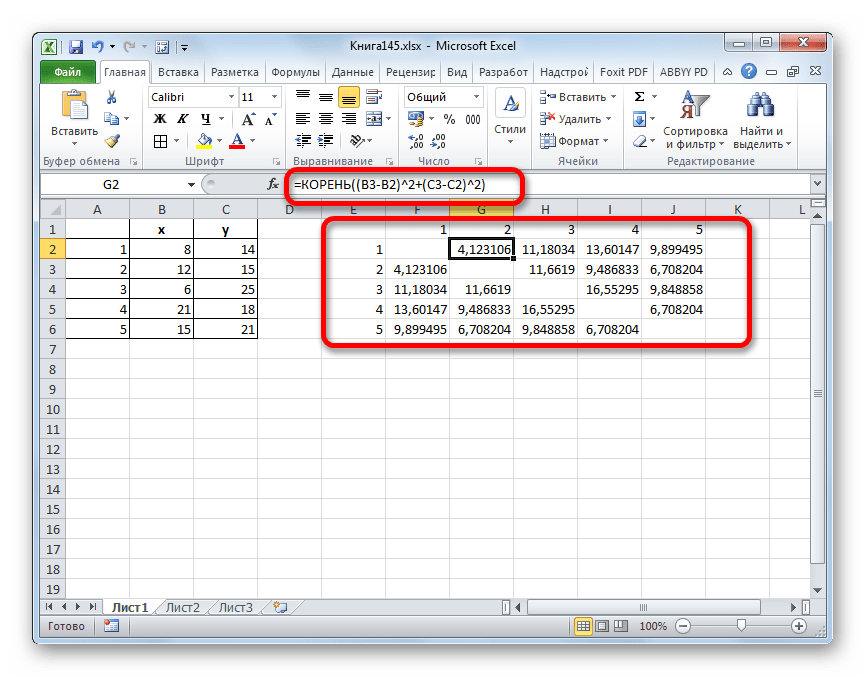
   =корінь ((x2-x1)^2 + (y2-y1)^2)


2. Дане значення обчислюємо між кожним з п'яти об'єктів. Результати розрахунку поміщаємо в матриці відстаней.

3. Дивимося, між якими значеннями дистанція найменше. У нашому прикладі &8212; це об'єкти 1 і 2 . Відстань між ними становить 4,123106, що менше, ніж між будь-якими іншими елементами даної сукупності.

4. Об'єднуємо ці дані в групу і формуємо нову матрицю, в якій значення 1,2 виступають окремим елементом. При складанні матриці залишаємо найменші значення з попередньої таблиці для об'єднаного елемента. Знову дивимося, між якими елементами відстань мінімально. На цей раз-це 4 і 5 , а також об'єкт 5 і група об'єктів 1,2 . Дистанція становить 6,708204.

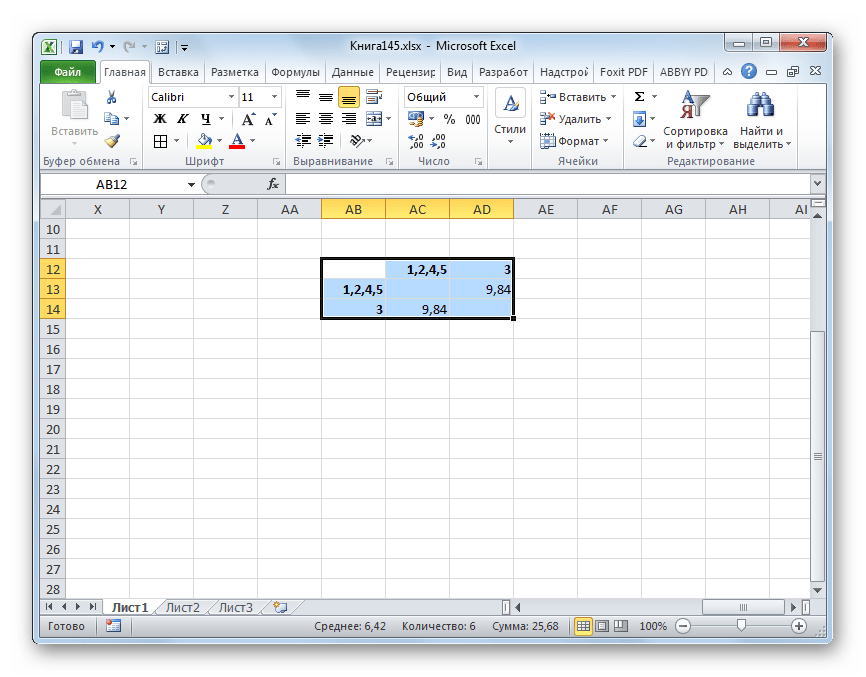
5. Додаємо зазначені елементи в загальний кластер. Формуємо нову матрицю за тим же принципом, що і в попередній раз. Тобто, шукаємо найменші значення. Таким чином ми бачимо, що нашу сукупність даних можна розбити на два кластери. У першому кластері знаходяться найбільш близькі між собою елементи – 1 , 2 , 4 , 5 . У другому кластері в нашому випадку представлений лише один елемент &8212; 3 . Він знаходиться порівняно на віддалі від інших об'єктів. Відстань між кластерами становить 9,84.

На цьому завершується процедура розбиття сукупності на групи.

Як бачимо, хоча в цілому кластерний аналіз і може здатися складною процедурою, але насправді розібратися в нюансах даного методу не так вже важко. Головне зрозуміти основну закономірність об'єднання в групи.